R中与xxx分布有关的函数包括：
dxxx(x)， 即xxx分布的分布密度函数(PDF)或概率函数(PMF)——option加log=TRUE可计算对数密度函数
pxxx(q)， 即xxx分布的分布函数(CDF)。
qxxx(p)， 即xxx分布的分位数函数, ， 对连续型分布，， 即的解。
rxxx(n)， 即xxx的随机数函数，可以生成个xxx的随机数。
R函数optim()、nlm()、optimize()可以用来求函数极值， 因此可以用来计算最大似然估计。 optimize()只能求一元函数极值。
函数optim()缺省使用Nelder-Mead单纯型搜索算法， 此算法不要求计算梯度和海色阵， 算法稳定性好， 但是收敛速度比较慢。 可以用选项method="BFGS"指定BFGS拟牛顿法。 这时可以用gr=选项输入梯度函数， 缺省使用数值微分计算梯度。 如：
\[ y=\omega^Tx=b \]
可否令模型预测值(上式中的 y，预测值)，逼近 \(y\) (真实标记，两个y含义不同)的衍生物呢？如果我们认为示例所对应的输出标记是指数尺度上变化，那我们就可以将输出标记的对数作为线性模型逼近的目标，即：
\[ \ln y=\omega^Tx \]
这就是对数线性回归，实际上是在试图让$exp{wTx+b}$接近 \(y\),仍然是线性回归，但实质上是输入空间到输出空间的非线性函数映射。
更一般地，考虑单调可微函数\(g(\cdot)\)，令：
\[ y=g−1(wt+b) \]
对数线性模型是广义线性模型在\(g(x)=\ln (x)\)的特例；
混合模型是一个可用来表示总体分布(distribution)中含有k个子分布的概率模型，也就是说混合模型表示了观测数据在总体中的概率分布，是一个由k个子分布组成的混合分布；
library("lme4")Warning: package 'lme4' was built under R version 4.1.2Loading required package: Matrixshowtext::showtext.auto()'showtext.auto()' is now renamed to 'showtext_auto()'
The old version still works, but consider using the new function in future codepoliteness <- read.csv("politeness_data.csv")
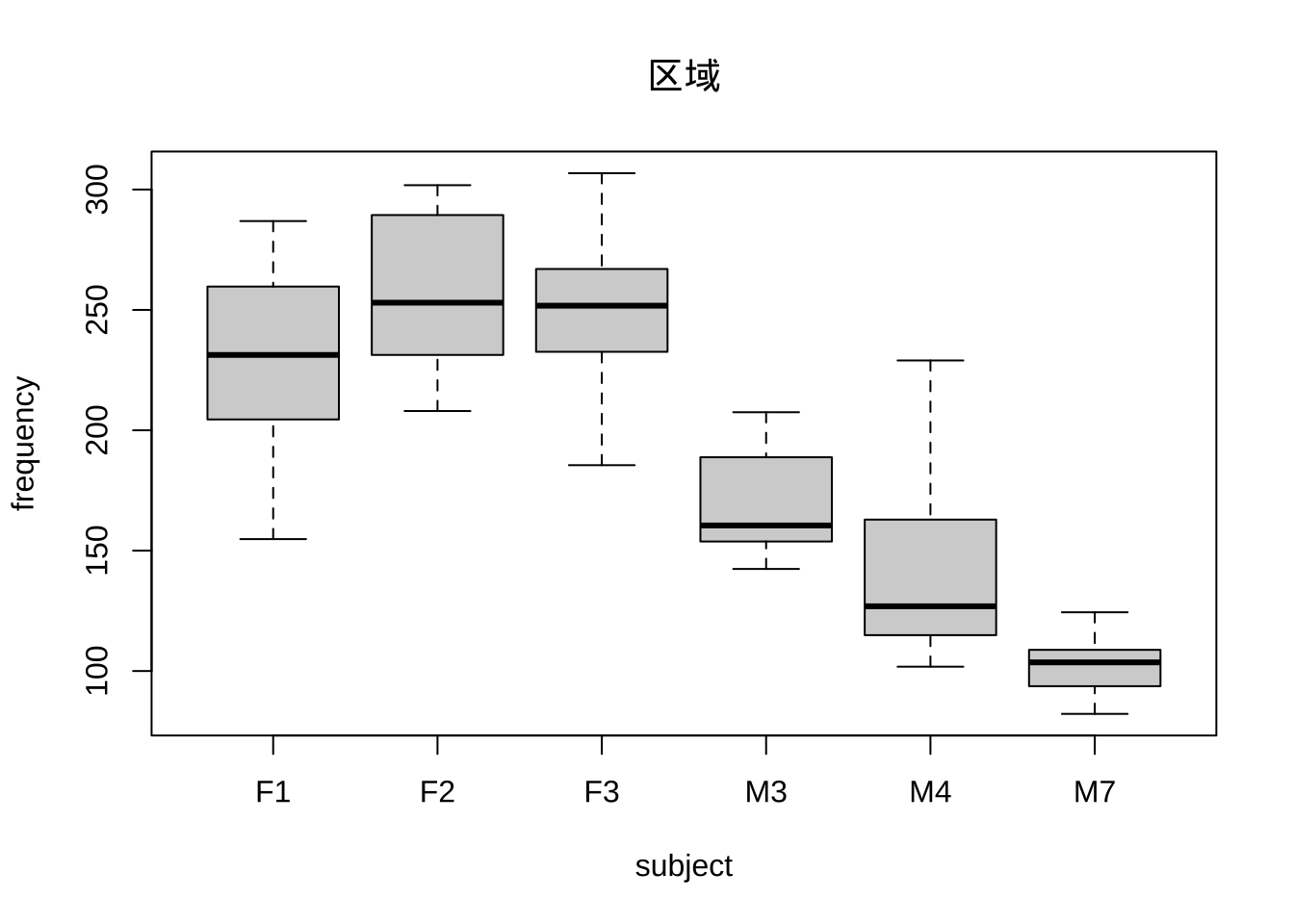
politeness <- politeness[-which(!complete.cases(politeness)),]boxplot(frequency~subject, politeness, main='区域')
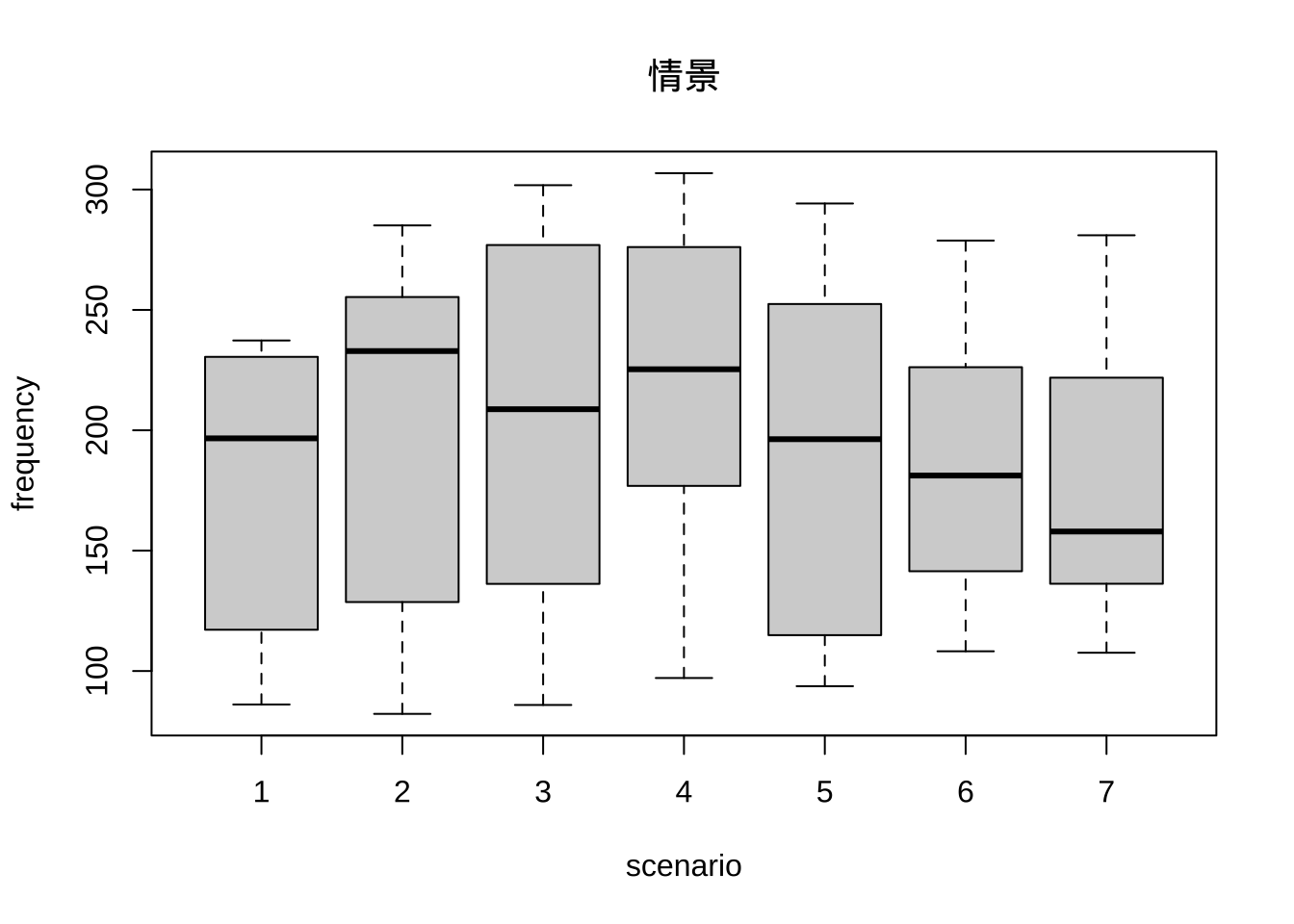
boxplot(frequency~scenario, politeness, main='情景')
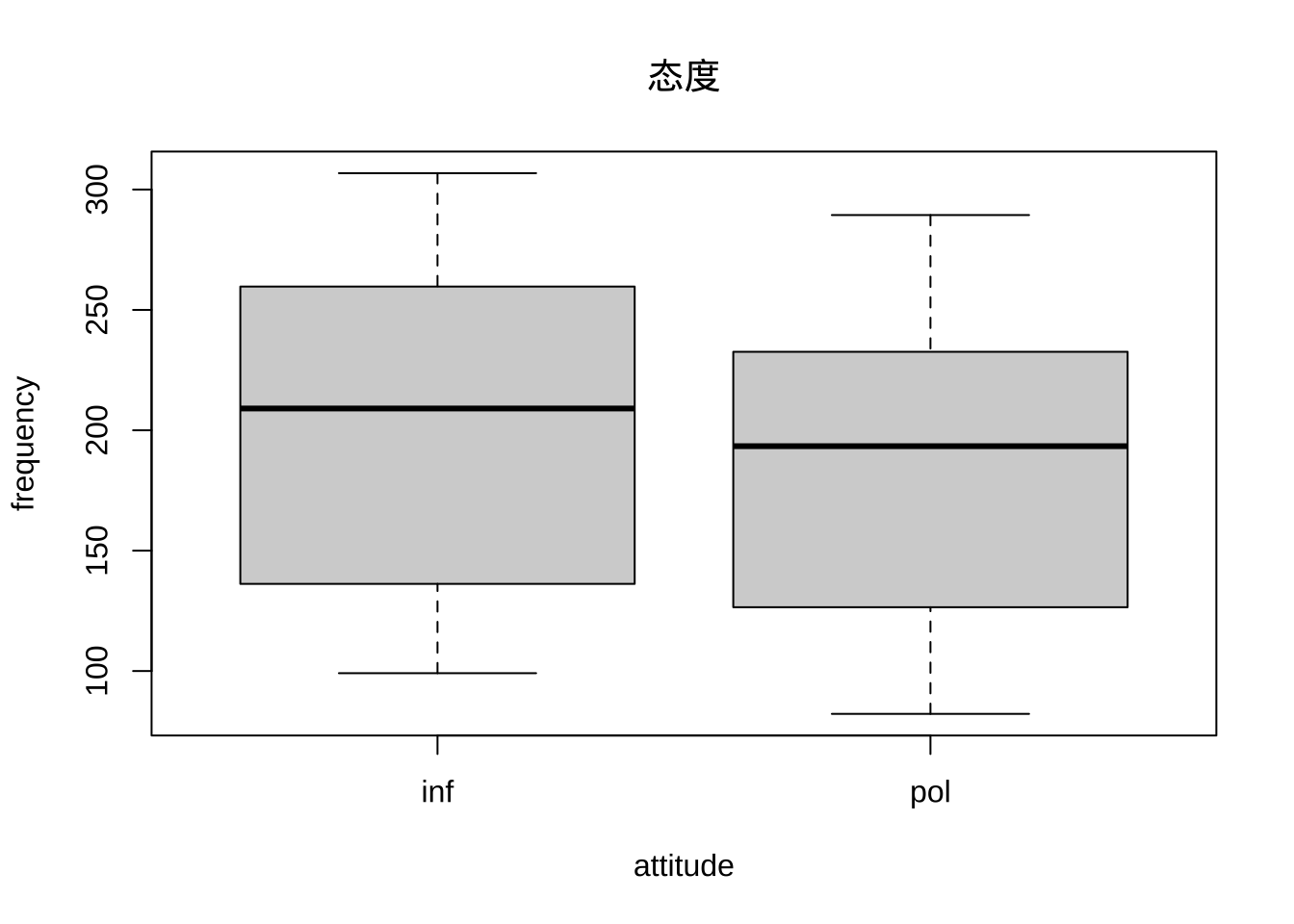
boxplot(frequency~attitude, politeness, main='态度')
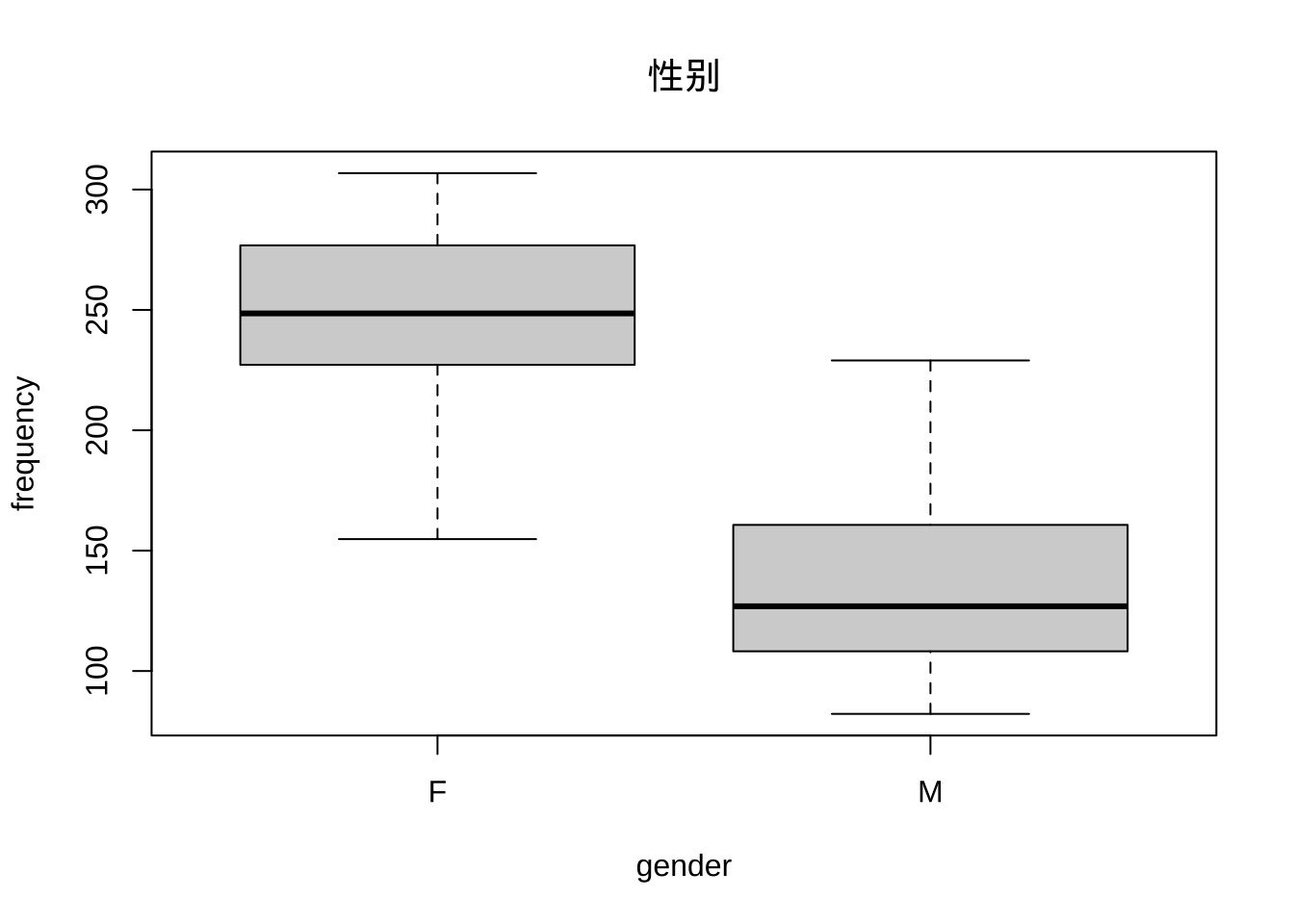
boxplot(frequency~gender, politeness, main="性别")
根据数据探索发现音调在不同区域存在一定程度的差异。
模型拟合
politeness.model <- lmer(frequency ~ attitude + gender + (1|subject) + (1|scenario),data=politeness,REML=FALSE)
summary(politeness.model)Linear mixed model fit by maximum likelihood ['lmerMod']
Formula: frequency ~ attitude + gender + (1 | subject) + (1 | scenario)
Data: politeness
AIC BIC logLik deviance df.resid
807.1 821.6 -397.6 795.1 77
Scaled residuals:
Min 1Q Median 3Q Max
-2.2958 -0.6456 -0.0776 0.5448 3.5121
Random effects:
Groups Name Variance Std.Dev.
scenario (Intercept) 205.2 14.33
subject (Intercept) 417.0 20.42
Residual 637.4 25.25
Number of obs: 83, groups: scenario, 7; subject, 6
Fixed effects:
Estimate Std. Error t value
(Intercept) 256.847 13.827 18.576
attitudepol -19.722 5.547 -3.555
genderM -108.517 17.571 -6.176
Correlation of Fixed Effects:
(Intr) atttdp
attitudepol -0.201
genderM -0.635 0.004逻辑回归假设数据服从伯努利分布，通过极大化似然函数方法，在运用梯度下降算法(Gradient Descent)求解得到参数值；
梯度下降：对于一个多元连续可导函数f(X),在xn处下降最快的就是\(x_n\) 梯度的反方向；故迭代策略：
\[ x_{n+1}=x_n-\alpha \nabla f(x_n) \]
其中\(\alpha>0\)控制下降步长
对数几率函数：是一种sigmoid函数，通过此函数来输出类别概率。
对数几率函数：\(y=\frac{1}{1+exp(-(w^Tx+b))}\)，其中y代表的是样本视为正样本的可能性，\(1-y\)代表的是视为负样本的可能性；
对数几率：定义为\(\log \frac{y}{1-y}=w^Tx+b\)，其中\(\frac{y}{1−y}\)称为比率；
决策边界：作用在n维空间，将不同样本分开的平面或曲面，在逻辑回归中，决策边界\(w^Tx+b=0\)
由对数几率函数输出正样本概率，得到对应关系: \[ P(y=1|x)=\frac{e^{w^Tx}+b}{1+e^{w^Tx}+b} \]
令\(P(y=1|x)=\pi(x)\)则对应的\(P(y=0|x)=\frac{1}{1+exp(w^tx+b)}\)
其中\(P(y=0|x)=1-\pi(x)\)
导入\(m\)大小的数据集，可写出似然函数： \[ l=\prod_{i=1}^m[\pi(x^{(i)})]^{y^{(i)}}[1-\pi(x^{(i)})]^{1-y^{(i)}} \]
对数似然函数就是：
\[ L(w)=\sum_{i=1}^m[y^{(i)}\log\pi(x^{(i)})+(1-y)^{(i)}\log(1-\pi(x^{(i)}))] \]
注意：在这里 \(y(i)\)为二分类值，同时还可以推广到多分类；
可化简为
\[ \sum_{i=1}^m\left[y^{(i)} \log \frac{\pi\left(x^{(i)}\right)}{1-\pi\left(x^{(i)}\right)}+\log \left(1-\pi\left(x^{(i)}\right)\right)\right]=\sum_{i=1}^m\left[y^{(i)}\left(w \cdot x^{(i)}\right)-\log \left(1+\exp \left(w \cdot x^{(i)}\right)\right]\right. \]
对数似然函数的对立面——损失函数
又称交叉墒损失函数，度量分布的差异性；
令
\[ h_\theta(x)=\frac{1}{1+\exp \left(-\theta^{T x}\right)} \]
使用 \(\theta\) 代替了 \([b,w_0,w_1,⋯,w_n]\)
交叉熵损失函数：
\[ J(\theta)=-\frac{1}{m} \sum_{i=1}^m\left[y^{(i)} \log _\theta(x)+\left(1-y^{(i)}\right) \log \left(1-h_\theta(x)\right)\right] \]
特别地对于Bernoulli分布，
$Pr(y:p)=py(1-p){1-y} $对于 $ y$
对数似然函数：
\[ l(\beta)=\sum^N_{i=1}{y_i logP_i+(1-y_i)log(1-P_i)} \]
\[P_i=1/1+exp(-(\beta\_1+\beta*2x*{2_i}+*\cdots+\beta*px{p_i}))\]
optim从initiate值开始进行迭代，所返回的值是。par作为初始值，开始迭代，返回的值是最优点点值
par元素表示最优解取值
value值表示目标函数值
counts代表调用目标函数与梯度函数的数目，可认为是迭代数目
convergence是收敛的代码
0表示成功完成了优化任务
1表示达到了达到了迭代上限而退出，关于迭代上限会在control参数的maxit元素进行说明
10表示退化(退化表示单纯型无法继续移动)的单纯型
51专指优化算法为L-BFGS-B的时候输出的警告信息。(L-BFGS-B为拟牛顿改进方法)
52专指优化算法为L-BFGS-B的时候输出的错误信息。
mtcars描述具有各种发动机规格的汽车的不同型号。 在”mtcars”数据集中，传输模式（自动或手动）由am列描述，它是一个二进制值（0或1）。 我们可以在列”am”和其他3列（hp，wt和cyl）之间创建逻辑回归模型。
# Select some columns form mtcars.
input <- mtcars[,c("am","cyl","hp","wt")]
print(head(input)) am cyl hp wt
Mazda RX4 1 6 110 2.620
Mazda RX4 Wag 1 6 110 2.875
Datsun 710 1 4 93 2.320
Hornet 4 Drive 0 6 110 3.215
Hornet Sportabout 0 8 175 3.440
Valiant 0 6 105 3.460我们使用glm()函数创建回归模型，并得到其摘要进行分析。
input <- mtcars[,c("am","cyl","hp","wt")]
am.data = glm(formula = am ~ cyl + hp + wt, data = input, family = binomial)
print(summary(am.data))
Call:
glm(formula = am ~ cyl + hp + wt, family = binomial, data = input)
Deviance Residuals:
Min 1Q Median 3Q Max
-2.17272 -0.14907 -0.01464 0.14116 1.27641
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 19.70288 8.11637 2.428 0.0152 *
cyl 0.48760 1.07162 0.455 0.6491
hp 0.03259 0.01886 1.728 0.0840 .
wt -9.14947 4.15332 -2.203 0.0276 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 43.2297 on 31 degrees of freedom
Residual deviance: 9.8415 on 28 degrees of freedom
AIC: 17.841
Number of Fisher Scoring iterations: 8每次拿到的数据都是一小部分的数据，小部分数据能够对所有数据有更好的代表，而最后的收敛过程很难被达到稳定的过程。
增强：收敛路径取平均值（原为不光滑）将平均值作为结果；
第三方的插件来帮助：learning rate 收敛过程，
calculus包，字符串输入进，
gradient： 可以求导之后的表达式，
deriv3
deriv :
numderiv 自变量带入，赋值之后可以直接形成结果。
一个建议：现在.R文件内写代码，然后再导入\.rmd文件中。
狭义的多重共线性：自变量的数据存在线性组合近似等于零，使得回归系数结果不稳定；
广义的多重：自变量之间有较强的相关性，自变量是联动的，互相之间有替代作用；
summary(lm(营业额～月收入，data=resturant))
如何识别
两个自变量之间的相关系数显著地不等于零，这个两个自变量之间就有广义的共线性；
F检验显著但单个回归系数不显著，可能是多重共线性；
如果有单个回归系数显著但是F检验不显著， 可能是由于多重共线性。
如果某些回归系数的正负号与通常的认识相反， 可能是由于多重共线性。
进一步确定的计量方法：
将自变量做因变量回归，得到一个复相关系数Ri2，接近1时候就说明多重共线性；
令\(x_i\)的容忍度(tolerance)1−Ri2，容忍度接近于0时候存在多重共线性；
还可以计算VIF：为容忍度的倒数
删去以后严重改变参数估计值的观测；
杠杆(leverage)指的是帽子矩阵的对角线元素\(h_{ii}\)
\[ \frac{1}{n}\leq h_{ii}\leq \frac{1}{d_i} \]
拟合值\(\hat y\)和实际观测值\(y\)之间的差值称为训练误差；
\[ e^t=y_t-\hat y_t \\=y_t-\hat\beta_0-\hat\beta_1x_{1,t}-\hat\beta_2x_{2,t}-\cdots-\hat\beta_kx_{k,t} \]
其中\(t=1,\cdots,T\)每个残差都是观测值中不可预测的部分；
时间序列数据来说，当前观测的变量值很可能与历史时段的变量值相似；
回归拟合：残差会出现自相关效应；
检验方法：Breusch-Godfrey检验；也称为LM检验；
异常值点：对模型的参数估计有重大影响的观测点；强影响点在x方向也是极端的异常值；
异常值：不正确的数据录入引起：
不平稳的时间序列会导致伪回归的出现：\(R^2\)值和高残差值自相关共存；
预测具有线性趋势和季度虚拟变量的回归：
模型中没有变量表示第一季度，因其他季度虚拟变量的系数是这些季度与第一季度之间差异的度量；
“趋势”“季节”不是R内的实际对象，需要这种方式时，由tslm()自动创建；
竞争对手的活动，广告支出等都会对于被预测变量产生影响；
\(R^2\)没有考虑到自由度的影响，在模型中增加任意一个变量，都会导致\(R^2\)值增大。
等效方法选择最小平方误差和(SSE)模型：
\[ SSE=\sum_{t=1}^Te_t^2 \]
在机器学习进行训练时候，为避免过拟合同时为检查模型的性能，往往会将数据分为三部分：训练集、验证集、测试集。但同时需要注意的是，最终模型和参数的选取会很大程度地以来对训练集和验证集的划分方式。 另一方面，训练数据越大，得到的模型效果往往越好，若将训练数据分为三部分，并没有很好的利用手头的数据，得到的模型就会受到影响。为解决该问题就使用交叉验证来将现有的数据进行”扩张”。
常用的一个交叉验证方法是LOOCV，只使用一个数据作为测试集，其余的数据作为训练集，这样就完成一次的训练，之后再进行第二次的训练。一直这样循环多次，每一次都得到一个MSE，之后再平均就是总体的MSE。
第二种为k折交叉验证：每次的训练集并不只有一个数据，而是有多个数据。实际上LOOCV是k折交叉验证的特例。k越大，每次的训练数据越大，模型的bias越小。
代码具体实现：
library(plyr)
CVgroup <- function(k,datasize,seed){
cvlist <- list()
set.seed(seed)
n <- rep(1:k,ceiling(datasize/k))[1:datasize] #将数据分成K份，并生成的完成数据集n
temp <- sample(n,datasize) #把n打乱
x <- 1:k
dataseq <- 1:datasize
cvlist <- lapply(x,function(x) dataseq[temp==x]) #dataseq中随机生成k个随机有序数据列
return(cvlist)
}k <- 10
datasize <- nrow(iris)
cvlist <- CVgroup(k = k,datasize = datasize,seed = 1206)
cvlist[[1]]
[1] 22 25 30 50 53 72 96 98 104 116 117 125 130 136 149
[[2]]
[1] 7 10 35 41 51 58 68 84 89 106 109 126 129 138 139
[[3]]
[1] 6 17 47 48 76 78 101 103 110 114 119 127 140 146 150
[[4]]
[1] 3 15 23 39 43 56 59 62 67 75 79 94 102 132 147
[[5]]
[1] 4 21 24 26 36 40 57 63 85 99 123 128 134 135 144
[[6]]
[1] 9 13 18 32 61 64 65 87 107 111 118 122 143 145 148
[[7]]
[1] 1 14 20 29 33 38 46 49 60 77 100 113 121 124 137
[[8]]
[1] 2 5 11 19 45 54 55 69 71 81 83 88 92 112 142
[[9]]
[1] 12 27 28 34 37 52 82 90 93 95 97 115 131 133 141
[[10]]
[1] 8 16 31 42 44 66 70 73 74 80 86 91 105 108 120AIC信息准则即Akaike information criterion，是衡量统计模型拟合优良性(Goodness of fit)的一种标准，由于它为日本统计学家赤池弘次创立和发展的，因此又称赤池信息量准则。它建立在熵的概念基础上，可以权衡所估计模型的复杂度和此模型拟合数据的优良性。
绘制AIC图形，检验预测的准确性：
\[AIC=2k-2\ln(L)\] - L是似然函数 - n是样本大小 - K是参数数量
增加自由参数的数目提高了拟合的优良性，AIC鼓励数据拟合的优良性但是尽量避免出现过拟合的情况。所以优先考虑的模型应是AIC值最小的那一个，假设在n个模型中作出选择，可一次算出n个模型的AIC值，并找出最小AIC值对应的模型作为选择对象。
T值较小时候，AIC准则总是倾向于选择更多的预测变量。一般而言，当模型复杂度提高（k）增大时，似然函数L也会增大，从而使AIC变小，但是k过大时，似然函数增速减缓，导致AIC增大，模型过于复杂容易造成过拟合现象。
贝叶斯信息准则(Bayesian Information Criterions, BIC)，其表达式为：
\[BIC=\ln(n)k-2\ln(L)\]
在R中使用的函数为AIC和BIC 具体格式为
AIC(object, …, k = 2)其中的object为传入的计算结果变量； k为数值，每个参数的惩罚量，默认为k = 2。
reg1<-lm(Fertility ~ . , data = swiss)
AIC(reg1)[1] 326.0716BIC(reg1)[1] 339.0226