9 随机模拟

模拟是指把某一现实的或抽象的系统的某种特征或部分状态，用另一系统（称为模拟模型）来代替或模拟。某些非随机的问题也可以通过概率模型引入随机变量，化为求随机模型的未知参数的问题。例10.1中用随机投点法估计就是这样的一个例子。

随机模拟积分也称为蒙特卡洛积分（MC积分）

set.seed(1)
I.true<-2^(3/4)*gamma(5/4)/sqrt(pi)
N=10000
yvec=abs(rnorm(N))^1.5
I.hat=mean(yvec)
sd.hat<-sd(I.hat)
sd.hat
I.residual<-I.true-I.hat

对于随机模拟的一些问题可以看成是$\theta=EY$的问题，设$Var(\theta)=\sigma^2$，生成样本独立同分布的$Y_i,i=1,2\cdots,N$用 \[ \hat \theta=\overline Y_N=\frac{1}{N}\sum^N_{i=1}Y_i \] 来估计$\theta$

$EY=\overline Y_N$时候，可以利用近似正态分布$N(\theta,\sigma^2/N)$

其中$\sigma^2$又可以用$S_N^2$来近似得到： \[ \frac{\hat \theta-\theta}{S_N/\sqrt{N}}\xrightarrow d N(0,1) \] 而同时对于估计$\hat\theta$中存在随机误差，度量方法： \[ RMSE=\sqrt{E(\hat \theta-\theta)^2} \] $E(\hat \theta)=\theta$故均方根误差RMSE： \[ RMSE=\frac{\sigma}{\sqrt{N}} \] 平均绝对误差： \[ MAE=E|\hat \theta-\theta|=\frac{\sigma}{\sqrt{N}}E|\frac{\hat \theta-\theta}{\sigma \sqrt{N}}| \]

9.1 高维定积分

计算一元的方法容易推广到多元的形式上；

设d元超矩形$h(x_1,x_2,\cdots,x_d)$定义于超矩形

\[ C=\{(x_1,x_2,\cdots,x_d)\}:a_i\leq x_i \leq b_i,i=1,2,3\cdots,d \] 同时函数有界；

对采样的理解:知道了一个变量的分布，要生成一批样本服从这个分布，这个就叫做采样；

定义：抽样从总体选择一组（样本），再从中收集可用于研究的数据。

总体(population)是从中抽取统计样本进行研究的元素或个体资源的集合；

9.2 从未知分布中采样

9.2.1 直接抽样

直接使用均匀分布；

通过对均匀分布的变换得到任意分布，间接的实现对其的采样；

变换方法：采用逆CDF变换法

假设x的概率密度为$ f(x)$ ，累计分布函数CDF为$ F(x)$，可通过以下步骤来得到非均匀随机样本：相当于已知y，通过反函数来求得x的对应值（一般只是适用于CDF，单调不减函数，可形成一一映射）

使用合适的PRNG（随机数生成器）从均匀分布采样$Z～U(0,1)$；
令$ X=F^{-1}(Z)$，X可认为是根据$ f(X)$得到的样本；

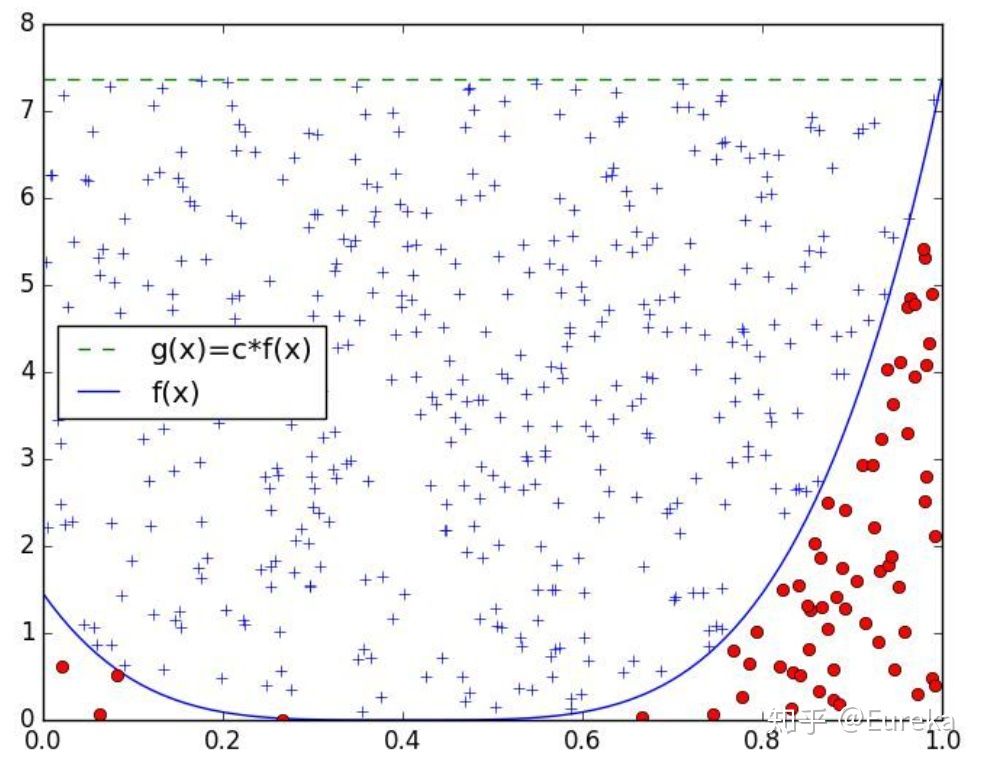
9.2.2 接受-拒绝抽样算法

v2-81ad256d0db58e18d2e2792c3968d57b_1440w

（之前一直困惑于怎么能够在每一个点找到对应的$ $去对应上目标密度）$ $是我们需要在每一个点所确定的，同时$ $也还是由[0,1]均匀分布生成的（与$$一一对应），因此这个思路就是落在目标分布内的accept，落在目标分布外的refuse；

v2-ba61bc580f87754f4e35675c6ac1b23c_1440w

一个直观的解释

9.2.3 间接抽样

9.2.4 MCMC采样

MC蒙特卡罗和马尔科夫

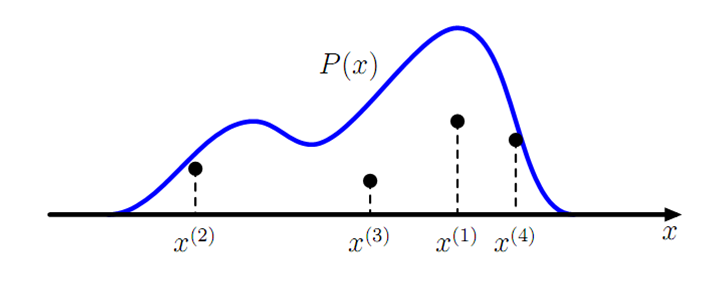
蒙特卡洛方法：给定概率分布$ p(x)$，通过抽样获得概率分布的随机样本，蒙特卡洛的核心就是随机抽样；

当$n$足够大时，可用均值近似$ _{i=1}^n $，这个就是蒙特卡罗方法的一般形式；

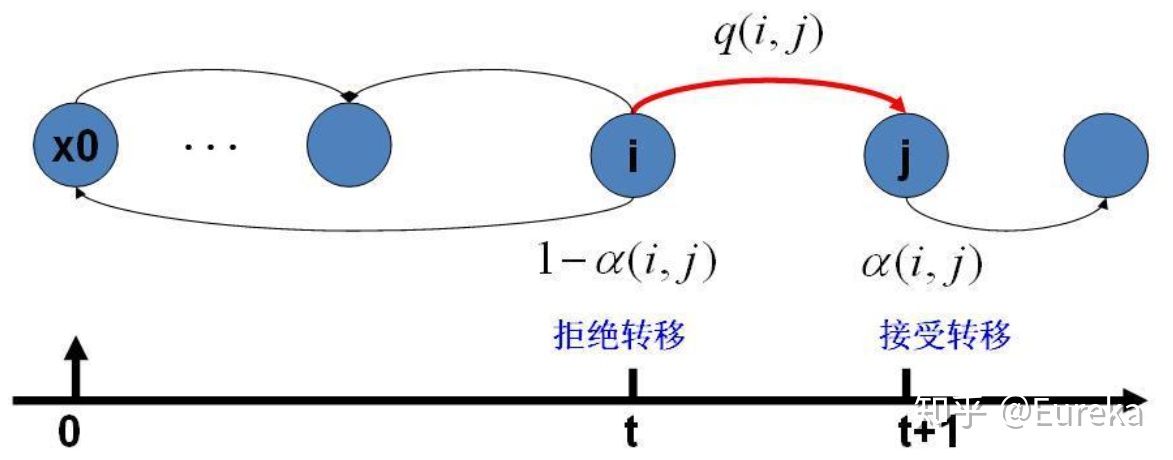
一般：目标平稳分布$\pi(x)$和某一个马尔科夫链状态矩阵$Q$不能满足细致平稳条件： \[ \pi(i)Q(i,j)\neq \pi(j)Q(j,i) \] 因此要使得等式两侧相等：引入$\alpha (i,j)$——总是被称为接受率

\[ \pi(i)Q(i,j)\alpha(i,j)=\pi(j)Q(j,i)\alpha(j,i) \] 由此又固定了马氏链矩阵$P(i,j)=Q(i,j)\alpha(i,j)$

v2-48086a0f62774d98f6b672b91d2dcda0_1440w

9.2.5 算法

输入任意给定的马尔科夫链状态转移矩阵Q，目标平稳分布$\pi(x)$，设定状态转移方程阀值$n_1$，需要的样本数$n_2$；
从任意简单概率分布得到初始值$x_0$
for t=0 in n_1+n_2-1

这个采样较难在实际中得到应用，$\alpha(x_t,x_*)$可能很小，导致大部分的采样值都被拒绝转移；采样效率低下；

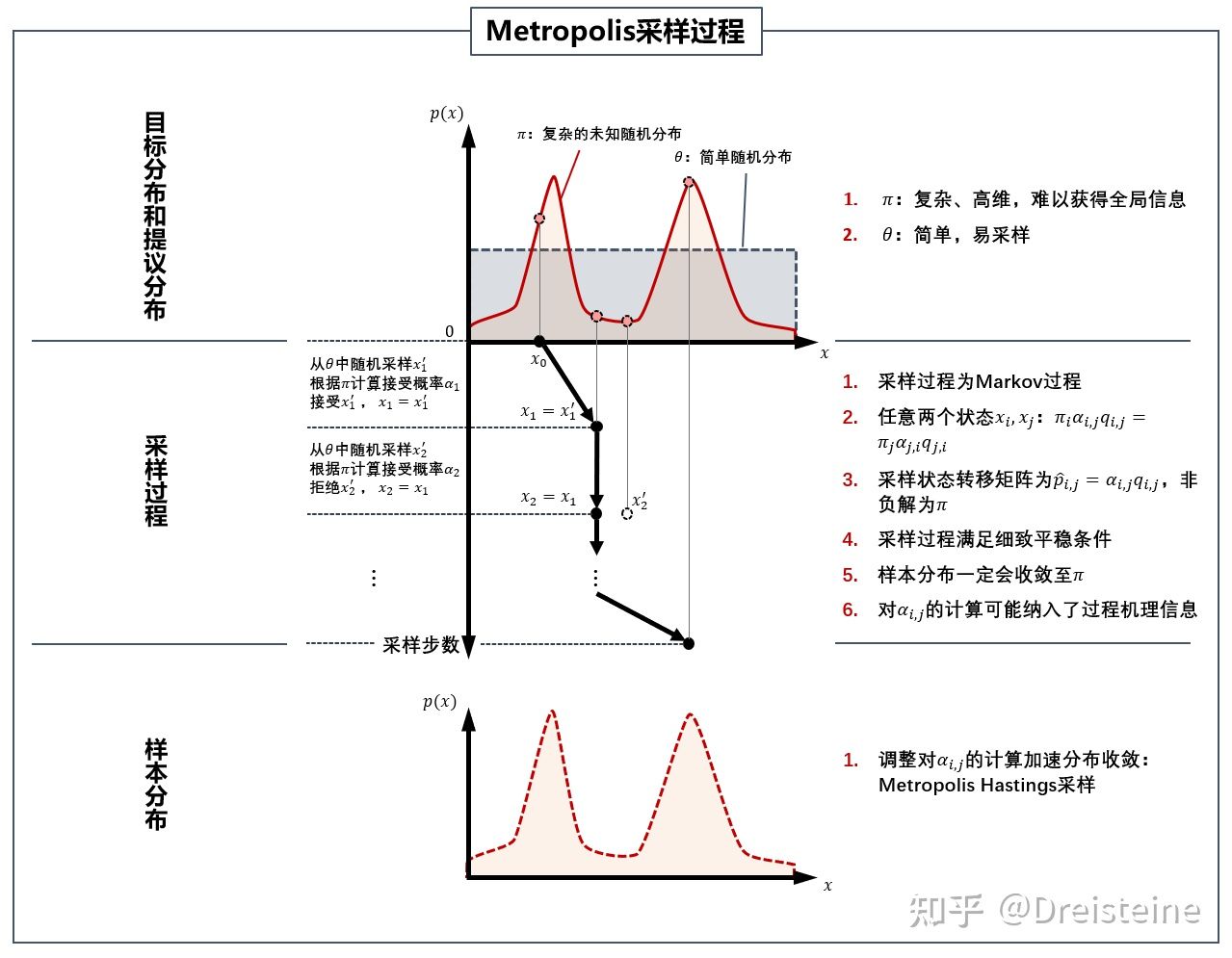
9.2.6 Metropolis algorithm

system statement s:系统中所有$n$个变量的取值组合，即 \[ s_i=[x_{1,i},x_{2,i},\cdots,x_{m,i}] \]
状态概率$\pi$：处于状态$s_i$的概率$\pi_i$
状态转移概率矩阵P：若不同状态之间的转移视为一个随机过程，其状态转移使用概率矩阵$P$表示，其中$P_{i,j}$表示过程从$i$到状态$j$的概率

\[ \sum_{j=1}^mP_{i,j}=1,for any i\in [1,m] \]

Markov链平稳性：对于一条非周期的Markov链，其任意两个状态保持联通，经过有限次数的转移可以达到，则存在一下的极限：

\[ \lim_{t\to \infty}P^t_{i,j}=\pi_j \]

9.2.7 Metropolis-Hastings algorithm

对于Metropolis算法的改进：接受概率$\alpha$可能很小，导致算法需要经历很多次的迭代才能达到平稳，MH就讲等式两侧的接受概率进行放大，将其中一个设置为1，就能保证每次迭代中接受新状态的概率越大，加速收敛；

\[ a_{j,i}=min\{1,\frac{\pi_jQ_{i,j}}{\pi_iQ_{j,i}}\} \]

https://zhuanlan.zhihu.com/p/37121528

https://cosx.org/2013/01/lda-math-mcmc-and-gibbs-sampling

统计学和机器学习：目的在于基于数据对概率分布的特征进行推断(induction)。

一般的均匀分布$ Uniform(0,1)$相对容易生成，进一步通过线性同余发生器生成伪随机数

9.2.8 一个概率分布样本

离散or连续都可以通过均匀分布的样本生成：如正态分布通过Box-Muller变换得到：

Box-muller：

\[\begin{align*} Z_0 & = \sqrt{-2\ln U_1} cos(2\pi U_2) \\ Z_1 & = \sqrt{-2\ln U_1} sin(2\pi U_2) \end{align*}\]

$ Z_0,Z_1$独立且服从正态分布；

其余的几个分布：指数分布，Gamma分布，t分布等都是可以通过类似的数学变换得到；离散的分布通过均匀分布更加容易生成；

MH采样：解决关于MCMC采样接受率过低的问题；

https://theclevermachine.wordpress.com/2012/11/05/mcmc-the-gibbs-sampler/

两边都进行扩大，细致平稳条件满足；

将等式扩大到C倍，使得$C\alpha(j,i)=1$（最大扩大为1）

提高了采样中的跳转接受率 \[ \alpha(i,j)=\min\{\frac{\pi(j)Q(j,i)}{\pi(i)q(i,j)},1\} \] 算法：

输入任意给定的马尔科夫链状态转移矩阵$Q$,目标平稳分布$\pi(x)$，状态转移次数阀值$n_1$需要样本数$n_2$
从任意简单概率的分布得到初始值$x_0$
for t=0 in $n_1+n_2-1$

从条件概率分布$Q(x|x_t)$得到样本值$x_*$
从均匀分布中采样$U～[0,1]$

9.3 马尔可夫迭代

9.3.1 马尔科夫链

假设某一时刻的状态转移概率只依赖于其前一个状态： \[ P(X^{t+1}|X,\cdots,X^t)=P(X^{t+1}|X^t) \]

状态转移矩阵也可求解：

\[ \pi_i =(Pr(X_i=0|X_0),Pr(X_i=1|X_0)) \]

最终得到的状态 $\pi$ 是该马尔可夫链的平稳分布

9.3.2 马尔可夫采样

细致平稳性条件

若非周期马尔科夫链状态转移矩阵$P$和概率分布$\pi(x)$对所有的$i,j$满足： \[ \pi(i)P(i,j)=\pi(j)P(j,i),for all i,j \] 只要我们找到了可以使概率分布$\pi(x)$ 满足细致平稳分布的矩阵$P$ 即可。这给了我们寻找从平稳分布 $\pi$ , 找到对应的马尔科夫链状态转移矩阵 $P$ 的新思路。

若得到某个平稳分布所对应的马尔可夫链的状态转移矩阵，就很好地可以求出样本集；

$q(j|i)=N(j|i,σ)$

一般不能满足细致平稳性：

进一步使得不等号变等号，需要乘以一个接受概率;

9.4 Gibbs采样

9.4.1 重新寻找合适的细致平稳条件

Gibbs是一种特殊的马尔可夫链算法；交替条件采样(alternating conditional sampling)交替指的是Gibbs采样的一种迭代；

已知观测值$y$，给定一个带有参数的向量$\theta=(\theta_1,\theta_2\cdots,\theta_d)$，若$\theta_j^t,j=1,2,\cdots,$d表示第j个参数$\theta_j$在第t次迭代的采样值，则该采样值随机地取自概率分布 \[p(\theta_j^t|\theta_1^t,\cdots,\theta_{j-1}^t,\theta_{j+1}^{t-1},\cdots,\theta_d^{t-1},y)\]

9.4.2 Gibbs步骤

仍然是拒绝-接受采样的思想

i9mg

通过固定其他维度逐一对某一维度进行采样；

关键在于找到合适的转移矩阵；

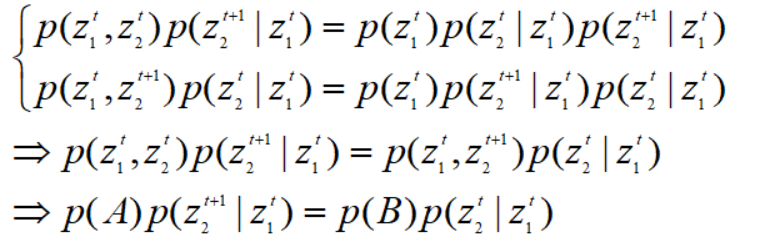
9.5 重要采样法

$I=\int _Ch(x)dx$中积分区域$C$任意形状，也可能无界；用直接平均值估计效果不好；对于一些样本量过大的来说，使用拒绝接受采样来说是不可取的；考虑非均匀抽样，$|h(x)|$大的地方密集投放点，就可以有效地投放样本。设$g(x),x\in C$为一个密度，其形状与$|h(x)|$相近，当$g(X)=0$时$h(x)=0$,当$||x||\to \infty$时候，$h(X)=o(g(x))$

基本思想：接受拒绝采样时候通过接受拒绝的方式对$ g(X)$来得到样本进行筛选；$g(X)$就是所说的试投密度或重要抽样密度；

函数$f(x)$在分布$ p(x)$下的期望可写为：

\[ E_p[f(x)]=\int_xf(x)p(x)dx \\=\int_xf(x)\frac{p(x)}{q(x)}q(x)dx \\=\int_xf(x)\omega(x)q(x)dx \\=E_q[f(x)\omega(x)] \]

其中：$\omega(x)$称为重要性权重；进一步可以用$f(x)$的样本来估计：

\[ \hat f_N=\frac{1}{N}(f(x^{(1)}\omega(x^{(1)})+\cdots+f(x^{(N)})\omega(x^{(N)})) \] 其中：$ x^{(1)},,x{(N)}$独立同分布$IID～q(x)$中抽出；

重要性采样方法程序；

set.seed(1)
N <- 10000
Ginv <- function(y) sqrt(1 + 3*y) - 1
X <- Ginv(runif(N))
eta <- exp(X) / (2/3*(1 + X))
I3 <- mean( eta )
var3 <- var(eta)

9.6 分层抽样法

将C上的积分分解为若干个子集的积分，使得$h(x)$在每一个子集上变化不大，分别计算各个子集的积分再求和，可提高精度；

一个例子

截屏2022-06-02 11.100.20

求定积分:

\[ I=\int _0^1h(x)dx \]

可以得到$I$精确值$I=0.05$，用平均值和分层抽样比较。

$(0,1)$区间随机抽取$N$点用平均值法得到$\hat I_2$，其渐近方差为

\[ Var(\hat I_2)=\frac{Var(h(U))}{N}=\frac {143}{150N} \]

9.6.1 R程序

rm(list=ls())

h<-function(x)ifelse(x<=0.5,1+0.1*x,-1+0.1*x)
I.true<-0.5
set.seed(1)
N=10000
eta=h(runif(N))
I2<-mean(eta)
sd2<-sd(eta)

I2
(I2-I.true)/I.true
sd2^2

eta1<-h(runif(N/2,0,0.5))
a<-0.5*mean(eta1)
eta2<-h(runif(N/2,0.5,1))
b=0.5*mean(eta2)
I5=a+b
I5