基本思想
基于距离的判别,马氏距离,减少样本方差之间的影响。
有时候的,多元回归,进行组合,表示为被解释变量。
假设条件
- 不存在多重共线性问题;
- 各组变量的协方差矩阵相等;
- 各变量之间多元正态分布;
- 基本要求:分组两个以上,案例规模1以上;解释变量可测。
距离判别法
根据类的中心距离进行判断类属。里哪里近就是属于哪一个类 欧氏距离: \[
d^2(x,G_1)=(x-\mu_1)'(x-\mu_1)
\]
两个总体情况
样本对类的距离进行比较; 当总体\(G_1\) 和
\[
d^2(X,G_1)=(x-\mu_1)'\Sigma_1^{-1}(x-\mu_1)\\
d^2(X,G_2)=(x-\mu_2)'\Sigma_2^{-1}(x-\mu_2)
\]
- 当总体不是正态分布时候,也可以用马氏距离来描述X到总体的距离。 - 构造判别函数:
\[
W(x)=\frac{1}{2}[d^2(x,G_2)-d^2(x,G_1)]
\]
进一步根据\(\Sigma_1,\Sigma_2,\Sigma\)之间的关系来进行分类:
若\(\Sigma_1=\Sigma_2=\Sigma\) 可以推出一个线性判别函数\(W(x)=(x-\overline \mu)'\Sigma^{-1}(\mu_1-\mu_2)\);
若\(\Sigma_1\neq\Sigma_2\) \(W(x)\)显然是一个二次函数 可以使用x的二次函数作为判别式。
\[
\hat \mu_1=\frac{1}{n_1}\sum_{i=1}
\]
若\(\Sigma_1\neq\Sigma_2\)
例子:比如要求一个马氏距离,假设服从同一个正态分布。 计算样本(6,8,8)到两组的马氏距离,判断属于哪个组?
df<-data.frame()
x<-c(6,8,8)
mu1<-c(8.4,8,7.5)
mu2<-c(4,3.5,4.5)
(x-mu1)^T
sig<-matrix(c(11.2,-3.5,2.5,-3.5,10,1.25,2.5,1.25,8.5),3,3)
print(solve(sig))
[,1] [,2] [,3]
[1,] 0.11184651 0.04406836 -0.03937668
[2,] 0.04406836 0.11923592 -0.03049598
[3,] -0.03937668 -0.03049598 0.13371314
ans1<-(x-mu1)%*%solve(sig)%*%(x-mu1)^T
ans2<-(x-mu2)%*%solve(sig)%*%(x-mu2)^T
对判别规则进行简化
Bayes判别方法
距离判别的不足,与总体中各自出现的概率无关,同时判别方法与错判之后的损失无关。
贝叶斯思想:假定对研究对象有一定对认知,再取得一定的样本。 先验概率分布,得到后验概率分布,各种统计推断。 - 贝叶斯+判别分析=贝叶斯判别
有k个总体\(G_1,G_2,\cdots,G_n\) 有p维密度函数,已知出现的概率为\(q_1,q_2,\cdots,q_k\)。 用\(D_1,\cdots,D_k\)表示一个划分方式,\(c(j|i)\)表示样本来自\(G_1\)而实际误判为\(G_j\)的损失。误判的概率为 \[
p(j|i)=\int_{D_j}p_i(x)dx
\] ECM(expected cost of misclassification)为 \[
ECM(D_1,\cdots,D_k)=\sum_{i=1}q_i\sum_{j=1}^kc(j|i)p(j|i)
\] 其中\(c(i|i)=0\) 总损失 根据这个表来计算属于哪一个组。
最大后验概率准则
k个总体,分布密度函数为\(f_1(x_1),f_2(x_2),\cdots,f_k(x_k)\)互不相同。 各自出现的先验概率为\(q_1,q_2,\cdots,q_k\)其中\(q_i\geq 0,\sum_{i=1}q_i=1\)。 - 最大后验概率是将样本\(x_0\)判别到后验概率最大的一类。
\[
P(G_l|x_0)=\frac{q_lf_l}{\sum_{j=1}^kq_kf_j(x_0)}=\max_{1\leq i\leq k}\frac{q_if_j}{\sum_{j=1}^kq_kf_j(x_0)}\Rightarrow x_i\in G_l
\]
p<-matrix(c(0,20,60,10,0,50,200,100,0),3,3)
q<-c(0.05,0.65,0.30)
f<-c(0.1,0.63,2.4)
sum(q*f*p[,1])
p1<-q*f
ans<-p1%*%p
which.min(ans) #return the index of minimum
Fisher 判别法
基本思想:将K组的p纬数据投影到某一个方向,对投影点来说使得各组之间尽可能的分开。然后选择合适的判别规则,将新的样品进行分类判别。
组间离差: \[
SSG=\sum_{\alpha=1}^kn_\alpha(a^T\overline x_i-a^T\overline x)^2
\] 组内离差:
\[
SSE=\sum_{\alpha=1}^k\sum_{i=1}^{n_\alpha}(a^T\overline x_i-a^T\overline x)^2\\=a^TEa
\]
优化方向:\(SSE\to \min;SSG\to max\)
\[
\Delta(\alpha)=\frac{a^T Ba}{a^T Ea}\to \max
\]
把来自2类的训练样本集划分为2个子集\(X_1\)和\(X_2\);
计算各类的均值向量\(\mu_i\);
计算各类的类内离散矩阵S_{wi},i=0,1,S_{wi}=_{xX_i};
计算类内总离散矩阵 ;
计算矩阵 的逆矩阵 ;
求出向量 (此处采用拉格朗日乘子法解出Fisher线性判别的最佳投影方向);
判别函数为 ;
判别函数的阈值 可采用以下两种方法确定:第一种是 ;第二种是 ;
分类规则:比较 值与阈值 的大小,得出其分类。
library(MASS)
data(iris)
diris<- data.frame(rbind(iris3[,,1], iris3[,,2], iris3[,,3]),species =rep(c(1,2,3), rep(50,3)))
head(diris)
Sepal.L. Sepal.W. Petal.L. Petal.W. species
1 5.1 3.5 1.4 0.2 1
2 4.9 3.0 1.4 0.2 1
3 4.7 3.2 1.3 0.2 1
4 4.6 3.1 1.5 0.2 1
5 5.0 3.6 1.4 0.2 1
6 5.4 3.9 1.7 0.4 1
sa<-sample(1:150, 75)
table(diris$species[sa])
z <- lda(species ~ ., diris, prior = c(1,1,1)/3, subset = sa,)
pre<-predict(z, diris[-sa, ])
- Prior probabilities of 先验概率
- groups:是各分类数据在总体中占得比例,是一个概率向量,用lda.sol$prior调用
- Group means:是每个分类的均值向量,用lda.sol$means调用
- Coefficients of linear
- discriminants:是降维矩阵,用lda.sol$scaling调用。这个矩阵的列空间是输入空间,行空间是输出空间,左乘一个行向量以将其降维
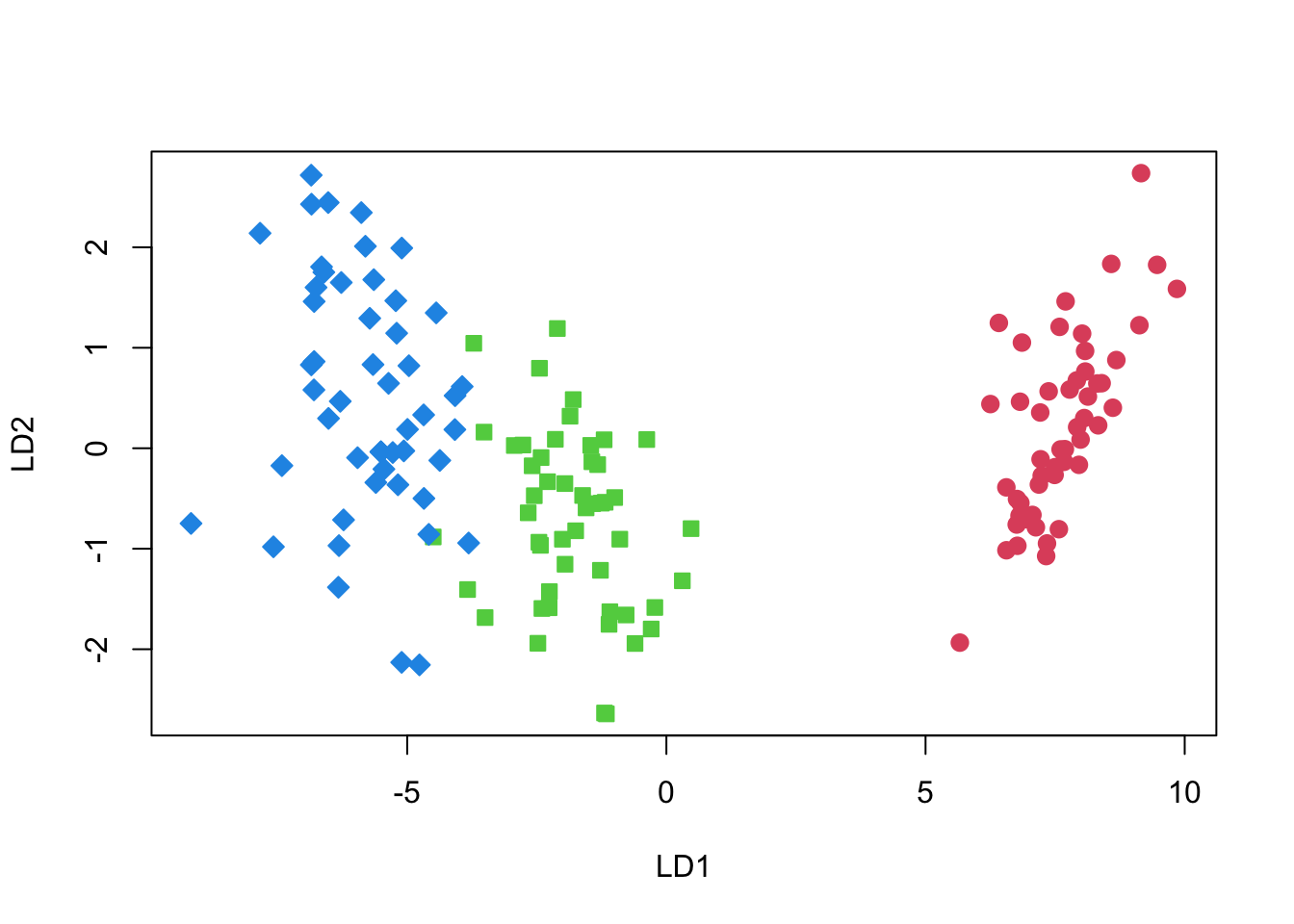
- Proportion of trace:降维后各分量的权重。在本例中,将4维向量降为2维,LD1占绝大比重。
irisdata=iris[,1:4]
irisgrp=iris[,5]
(lda.sol=lda(irisdata,irisgrp))
Call:
lda(irisdata, irisgrp)
Prior probabilities of groups:
setosa versicolor virginica
0.3333333 0.3333333 0.3333333
Group means:
Sepal.Length Sepal.Width Petal.Length Petal.Width
setosa 5.006 3.428 1.462 0.246
versicolor 5.936 2.770 4.260 1.326
virginica 6.588 2.974 5.552 2.026
Coefficients of linear discriminants:
LD1 LD2
Sepal.Length 0.8293776 0.02410215
Sepal.Width 1.5344731 2.16452123
Petal.Length -2.2012117 -0.93192121
Petal.Width -2.8104603 2.83918785
Proportion of trace:
LD1 LD2
0.9912 0.0088
result = predict(lda.sol, irisdata)
table(irisgrp, result$class) #$class是预测结果
irisgrp setosa versicolor virginica
setosa 50 0 0
versicolor 0 48 2
virginica 0 1 49
P = lda.sol$scaling
# 将均值向量降维
means = lda.sol$means %*% P
# 加权平均的出总的降维均值向量,权重就是lda.sol$prior
total_means = as.vector(lda.sol$prior %*% means)
n_samples = nrow(irisdata)
# 把样本降维并平移
x<-as.matrix(irisdata) %*% P - (rep(1, n_samples) %o% total_means)
plot(x, cex=1.2,
pch=rep(21:23, c(50,50,50)),
col=rep(2:4, c(50,50,50)),
bg=rep(2:4, c(50,50,50)))