10 优化算法

10.1 牛顿优化算法

\[ x_{n+1}=x_n-(\frac{\partial^2 f(x)}{\partial x \partial x'})^{-1}\frac{\partial f(x)}{\partial x} \]

Rprof

较高波峰和波谷

1. 选择初始猜测点 x0x0，设置 n=0n=0。
2. 按照以下迭代过程进行迭代：
xn+1=xn−f′(xn)f′′(xn).xn+1=xn−f′(xn)f′′(xn).

1. 计算
   |f′(xn+1)||f′(xn+1)|
   1. 如果 |f′(xn+1)|≤ϵ|f′(xn+1)|≤ϵ，停止迭代；
   2. 否则，返回第 2 步。

https://blog.csdn.net/zhangdamengcsdn/article/details/80200059

R中求偏导的方法:R使用D() 来求一元函数的导数，用deriv() 来求多元函数的偏导数；

10.2 Quasi-Newton Methods

对于牛顿迭代来说，难以求出二阶导数（样本空间较大时）

取消二阶导，直接运用一介导来求解；

10.3 BGFS算法（准牛顿算法）

以其发明者Byoyden,Fletcher,Goldfarb,Shanno命名；

BFGS算法以下算法来近似Hessian矩阵；

\[ B_k\approx H_k \]

Origin: \[ B_0=I \]

10.4 最优梯度下降算法

10.4.1 原理

梯度下降的目的，就是为了最小化损失函数

\[ L(w,b)=\frac{1}{N}\sum^N_{i=1}(y_i-f(wx_i+b))^2 \]

要控制两个过程：即控制两个参数，输入的信号量的权重（weight/w）另一个为调整函数与真实值距离的偏差（bias，b）

通过梯度下降方法来实现，使得损失函数的值变得越来越小；

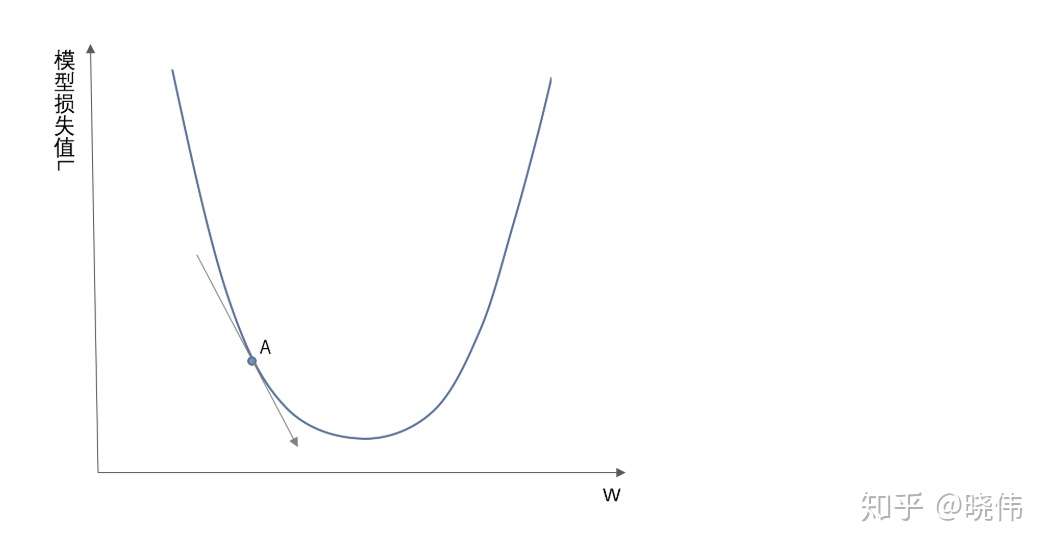
学习率(learning rate)

\[ w_{i+1}=w_i-\alpha *\frac{dL}{dw_i} \]

10.4.2 梯度下降的过程

10.4.2.1 更新策略

\[ x_n+1=x_n−\alpha\nabla f(x_n) \]

10.5 随机梯度下降算法

梯度下降算法通常收敛速度较慢，因为在每次迭代中对每个样本值都需要计算梯度，在样本量较大时计算量会随之增大。随机梯度下降算法的思想是在算法的每次迭代更新时只考虑一个样本。以线性回归模型为例，就是将梯度下降算法中的

将训练数据随机排序，然后重复第2步直至收敛。
抽取一个随机样本 $i\in\{1,2,⋯,n\}$，根据下式对$\beta$进行迭代。

\[ \beta=\beta-\alpha\nabla J(\beta)i \]

10.6 Nelder Mead算法（单纯形法）

R中optim()的默认算法；

算法思路：从n维单纯形定点出发（在矩阵上的表示就是非奇异矩阵）；进一步计算每个单纯形点点函数值$ f(x_j)$，从中再选出对于我们迭代过滤的点，即表现最差的点；

进一步计算剩下n个点的中心点，再代入过滤点生成新点：

$x_r=x_0+α(x_0−x_n+1)$

通常取$\alpha =1$

在$R^n$空间中，一点的迭代通常会有两种情况：

$f(x1)≤f(xr)<f(xn)f(x1)≤f(xr)<f(xn)$，这种情况下 $xr$ 既不是最佳点也不是最差点，将 xn+1 替换为 xrxr，形成新的单纯形，回到第一步。
$f(xr)<f(x1)$,$f(xr)<f(x1)$，即 $xr$ 为最佳点，那么在这个方向上继续延伸，得到延伸点（Expansion Point）：通常取$\gamma=2$
$f(xr)≥f(xn)$,$f(xr)≥f(xn)$，即 $xr$ 为最差点，这意味着在 $xn+1$ 和 $xr$ 之间可能存在谷点，这时寻找收缩点（contraction point）：